请原谅我今天,冒昧地拉着你聊这个话题——数学。
数学这个话题,是我一直想分享,但又不敢分享的。
为什么?
因为,它太难了。
这两个字,简直就是一个抽象扭曲的魔鬼。甚至,有同学在报考大学专业的时候说,只要不学数学,选什么专业都行!
我理解。我明白。
可是,对大部分人来说,学数学,不是为了解开数学题,不是为了当数学家,而是为了培养数学思维。
数学思维,不仅能让你登上更高的高度,开拓你的眼界,也能够帮你建立一些正确的常识,让你少走一些弯路,并且让你在人生的每一个岔路口,有更多更多的选择。
今天我能够给企业做战略咨询,能够快速洞察一件事物的本质,其实,最最根本的能力,就来自于数学思维。
可是,数学还是太难了,我学不会怎么办?
解数学题也许很难,数学考试拿满分也许很难,但是,只要你愿意,培养自己的数学思维其实并不难。
今天的文章会有些长,内容有点多,但我会尽可能地用我绵薄的知识,把它讲得更好玩一些。
相信我,坚持看完,你会有一些小启发的。
1
什么?你还是抵触?为什么要抵触?
好吧。我试着猜猜,你看看是不是这么回事。
很多人学了十几年的数学,一离开学校,根本不知道数学到底有什么用。
语文,也很难学。但学好语文,起码能写出动人的情书。
英语,还是很难学。但学好英语,起码出国旅游的时候不需要请翻译。
数学…我一直觉得数学挺简单的,加减乘除。
直到…三角函数出现在我生命里的那一天。
(三角函数,图片来自网络)
自打Sin和Cos出现起,老师不再亲切了,课本变成天书了,我的世界也开始变得灰暗了。谁能告诉我,学这些三角函数有什么用?我保证以后不碰三角形的物体还不行吗?
为何数学恐怖如斯?
不妨试着想象一下,数学,就是一座高楼大厦。
那,这座大厦是怎么一步一步被搭建起来的呢?
你看,数学的世界里,有很多的公理。
比如说,任意两个点可以通过一条直线连接;任意线段能无限延长成一条直线;给定任意线段,可以以其一个端点作为圆心,该线段作为半径做一个圆;所有直角都全等;若两条直线都与第三条直线相交,并且在同一边的内角之和小于两个直角和,则这两条直线在这一边必定相交。
头都晕了!
但你可能已经想到了。是的,这是欧氏几何的5条基本公理。
从这5条公理出发,用纯逻辑推理的方法,可以推导出无数条定理。
比如说,每一条线的角度都是180度;三角形的内角和等于180度;过直线外的一点,有且只有一条直线和已知直线平行……
这就是一幢名叫欧氏几何的大厦。
你发现了吗?数学,本来就是逻辑的产物。
可如果,我从这幢大厦里,随机地抽出一块产物递给你呢?
这块产物原本是用来解决一个什么样的问题的?不知道。是从哪条公理推导出来的?也不知道。是怎么推导出来的?还是不知道。
不知道怎么办?
不需要知道,记下来就行了。可谁又能记下一整座大厦呀。
学的时候昏昏沉沉,考的时候自然天旋地转。
可是,你相信吗?
所有的数学,都是为了解决有趣的问题。
你不信?
我举个例子。
2
先抛一个问题吧。
你知道,为什么计算机要用二进制吗?
好吧。这个问题可能有点简单。因为计算机的各个门电路,只有“开”和“关”两种状态。那就用“0”来表示关,用“1”来表示开。简单、方便。
既然这么简单,可为什么绝大部分的国家,到最后采用了十进制呢?
是为了解决计数的问题。
我今天采回了一批果子,和你们共享。你家分多少颗,他家分多少颗,这就得有个数。
怎么记这个数呢?用计算器吗?进制诞生的时候,不光是没有计算器,恐怕是连本子都没有。
那怎么办?
于是,拥有高等智慧的人类,不约而同地望向了自己的双手。
这十根手指,不就是天赐的计算器吗?分一颗,掰一根。分两颗,掰两根。
分十一颗…好吧,再掰一轮。
可是,既然十进制是天赐的宝物,为什么还有十二进制呢?
比如说,星座,是十二进制的。生肖,也是十二进制的。
为什么?是因为古代有一个特殊的种族,长了十二根手指吗?
那倒不是。其实答案,依然在你的手上。
如果,你不嫌弃的话,我想邀请你和我一起做这样的一套动作。
第一步,张开你的右手。
第二步,移动你的大拇指,放到食指最下面的指节上,并默念:1。然后向上移动你的大拇指,放到食指中间的指节上,并默念:2。再向上移动,并默念:3。
第三步,移动你的大拇指,放到中指最下面的指节上,并默念:4。
……
最终,你会成功地数到12。
怎么样?算出我的财运了吗?能和我说说吗?
不闹了。这就是十二进制。不是有人长了十二根手指头,而是因为有的人习惯掰手指,有的人习惯点指节。
那那那…为什么还有六十进制呢?
比如说,闹钟,是六十进制的。甲子纪年法,也是六十进制的。
不卖关子了。答案,仍然在你的手上。
有的人习惯掰手指,有的人习惯点指节。那把“掰手指”和“点指节”结合一下,就是六十进制了。
你看,用右手掰手指,能计五个数。用左手点指节,能计十二个数。
是的,你已经想到了。五乘以十二,就是六十。
你再猜猜,这个世界上,有没有二十进制呢?
当然。人类有双手双脚,共计二十个指头,当然也会有二十进制的计数法。据说,玛雅人用的就是二十进制。
至于二十进制为什么很少被使用的话…
大概是因为用脚计数不文明吧。
二进制,十进制,十二进制,六十进制,二十进制,都是为解决有趣的问题而生的。
想象一下,如果小学的数学老师,真的带着你掰了一节课的手指,你还会忘记这些知识吗?
我猜,不会的。因为你知道,那些数学公式,投射到现实世界里,到底是为了解决一个什么样的问题。
我再举个例子。
3
也许,你觉得自己的数学成绩是一场灾难。
可你知道吗?和世界上其他国家的同学比起来,你有着得天独厚的优势。
为什么?
因为汉语,在帮你学数学。
看到这里,你可能会有点疑惑。学数学,和汉语有什么关系?
我举个例子。
如果你愿意的话,请口算一下,13乘以9,等于多少?
没错,是117。
请问,你是怎么算出来的呢?
我猜猜看,是不是“三九二十七”,“一九得九”,二十七加九十,得出的117?巧了,我也是这么算的。
我想再问一个“无聊”的问题:这个“三九二十七”,是哪来的?
来自一张流淌在血液里的表格——九九乘法表。
是的。我和你一样,也背过这张九九乘法表。我们今天所拥有的口算能力,都建立在这张表的基础之上。
可是你知道吗?如果你在一些外国友人的面前,通过口算得出了13乘以9等于117,他会像看神仙一样看着你的。
为什么?因为在这个世界上的很多国家,是没有九九乘法表的。
没有九九乘法表?那怎么口算?
挺新奇的。我试着讲给你听。
比如说,古埃及人。
很久很久以前,古埃及人还生活在国王的统治之下。耕田种地,那是要交税的。
怎么交?
按土地面积交。横着走13步,竖着走9步,就是这块土地的面积。
可是,没有九九乘法表,13乘以9要怎么算呢?
古埃及人,是用堆石头的方法来解决的。
怎么堆?
第一行,先在左手边,放下13颗石子。再在右手边,放下1颗石子。
那第二行呢?要怎么堆?
翻倍。先在左手边,放两次13颗,也就是26颗。再在右手边,放两次1颗,也就是2颗。
第三行,也是同样的道理。左手边是26的翻倍52颗,右手边是2的翻倍4颗。
那要堆到什么时候?
堆到右手边能加出9的时候。
你看,右手边的第一行,是1颗石子。第四行,是8颗石子。一共就是9颗。
左手边的第一行,是13颗石子。第四行,是104颗。一共就是117颗。
天啊,这也太神奇了。
还有吗?
再比如说,俄罗斯人。
战斗民族是怎么解决乘法问题的呢?
第一行,先在右手边,写上13。再在左手边,写上9。
第二行,在右手边减半(6.5),但只取整数,写上6。再在左手边,翻倍,写上18。
第三行,右手边就是3,左手边就是36。
第四行,右手边就是1,左手边就是72。
有趣的事情又出现了。
右手边,有三个奇数:13,3,1。三个奇数的左手边,对应着三个数字:9,36,72。
9+36+72。没错,也是117。
其实,不光是古埃及和俄罗斯,这个世界上,还有各种各样五花八门的乘法计算方式。
虽然,这些计算方式看上去很“怪异”。但是,准确且有效,就是计算的意义。
可是,在效率上,几乎没有任何一种计算方式,能够媲美九九乘法表。
既然如此,没有九九乘法表的国家,为什么不引进呢?
答案是,语言。
汉语中的数字,一、二、三…九,都是单音节的。英语中的数字,one,two,three…nine,既有单音节,又有双音节。
我们小时候背的九九乘法表,朗朗上口,音律感特别强。
想象一下,英语世界的孩子们要是背九九乘法表,那得乱成什么样?
俄罗斯的孩子说,你们聊,我先走了。
你发现了吗?数学的背后,就是一个又一个有趣的问题。
数学,就是用来窥探万物本质的。
4
我到今天还能记起,我在南京大学的第一堂数学课。这堂课的名字叫做“概率”。
概率?这不是高中就学过的知识吗?
于是,数学老师用“条件概率”,给了我们一个下马威。
什么是条件概率?
老师出的那道题,是这么说的。
“有一对父母,生了两个小孩。已知其中一个是女孩,请问,另外一个也是女孩的概率是多少?”
非男即女,50%吗?这应该明显不对,这道题不可能这么简单吧。
25%?也不对。
那,怎么来思考这个问题呢?
首先,站在最顶端的位置(父母)来思考。生孩子,肯定是有先后的。先生一胎,再生二胎。非男即女,所以有四种不同的结果:男男、男女、女女、女男。每种结果的可能性各占25%。
这应该挺容易理解的。
但是,题目中有一个隐藏的条件:已知其中一个是女孩。
什么意思?
简单来说就是,不符合这个条件的样本“男男”,就不在讨论的范围之内。
也就是说,只有“男女、女女、女男”三个样本。
所以,其中一个是女孩,另外一个也是女孩的概率,是三分之一。
这就是条件概率。
头又开始痛了…
不是说,窥探万物本质吗?条件概率,能窥探什么?生二胎的心理预期吗?
别着急。我斗胆试着点一点。
假如,你想知道中国有多少孩子喜欢书法。
如果你在学校里发问卷,调查的结果可能是20%。如果你在兴趣班里发问卷,调查的结果大概会高一些,40%。如果你在书法班发,那结果也许就是80%。
为什么?
因为“条件”变了。
那你猜猜看,哪个行业的人,用“条件概率”用得最熟练?
好吧。小标题已经出卖了我。
你大概也有过这样的经历。
你接到一个陌生的来电,电话的那一头说,我是你的领导,我现在遇到了一点情况,给我转个几万块钱,周一我到办公室还你。
浓重的口音,磕巴的发言,一点专业水准都没有。简直是把“骗子”两个字写在了脸上。
这么蠢,能骗得到人吗?
还真能。因为骗子特别擅长用“条件概率”来管理他的样本。
什么意思?
在骗子眼里,这个世界上只有两种人。一种是容易上当的,一种是不容易上当的。
和不容易上当的人通上一个小时的电话,你还是骗不了他。
可如果,把这一个小时花在容易上当的人身上,成功率就能大大提高。
也就是说,骗子要提前把容易上当的人,筛选出来。
可是,容易上当的人,也不会把这几个字写在脸上啊。怎么筛选?
一开始就表现得像一个骗子。
我都表现得这么明显了,你居然还能跟我聊下去?
要么,你是小爱同学。要么,你就是我的目标客户。
如果你一听就知道我是骗子,很生气,啪的一声挂掉了电话。
太好了,反正我也骗不到你,我们各自安好,不要浪费彼此的时间。
聪明人,一下子就被筛除掉了。
这就是骗子的小把戏。
5
聊到概率,就绕不开一项实验。
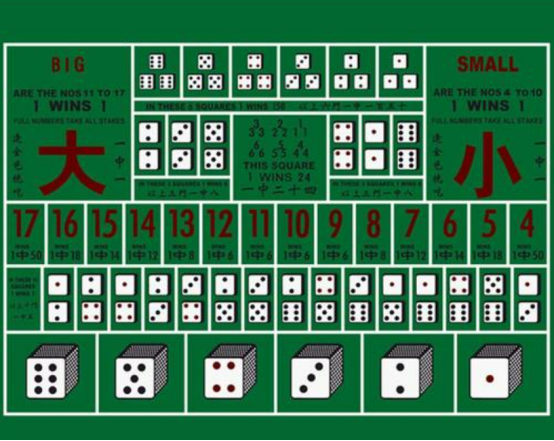
这项实验叫做:带编号的立方体重复性概率试验。
坊间俗称,赌大小。
具体怎么赌呢?
就像电视剧里播放的那样。庄家把三个骰子放进骰盅,用随机的力度、幅度、次数摇动骰盅,并在随机的时间之后停止。
然后,请下注。
(赌大小赔率,图片来自网络)
是买大小好呢?还是买三个六好呢?
这就涉及到了一个数学概念——数学期望。
怎么算呢?
如果,你花一块钱买了大。
买中,就能收益一块钱。买失,就会损失一块钱。买中大的概率,是48.6%。(为了减轻头疼的症状,计算过程就不展开了)
所以,买大的数学期望是:1*48.6%+(-1)*51.4%=-0.0278。
这就意味着,如果你不停地买,不停地买,每买一次,就要亏掉0.0278块钱。
如果,你花一块钱买了三个六。
买中,太厉害了,收益149块钱。买失,还是损失一块钱。看上去,是不是很划算?
可是,买中三个六的概率,只有可怜的0.46%。
所以,买三个六的数学期望是:149*0.46%+(-1)*99.54%=-0.31。
这就意味着,如果你不停地买这种以小博大的三个六,每买一次,就要亏掉0.31块钱。
买大小,买中的概率更大,可还是在亏损。
买三个六,看起来很划算,其实比买大小亏得更多。
那怎么买?
这还用想?这是赌徒的迷宫,当然是站起来就走啊!
这就是“久赌必输”的逻辑。
6
闹了半天,数学书里的这些东西,难道就是用来做坏事的吗?
闹了半天,数学教的这些概率、数学期望,就是用来做坏事的吗?
当然不是。商业的底层逻辑,同样是数学。
比如说,风险投资。风投,就是一种特别典型的,系统性地用概率和数学期望来赚钱的方式。
什么意思?
假如一家创业公司,成功的概率有5%,成功之后,利润是成本的20倍。
那么,这家创业公司值不值得投资?
理论上来说,值得。
为什么?
因为它的数学期望大于1。
可是,即便一件事情的数学期望大于1,这件事情值得去做。
但是对于这位创业者来说,成功的概率只有5%。
这个概率实在是太小了。
他的成功,是极度不确定的。
5%的成功率,就意味着还有95%的概率会失败。
也就是说,我投资他,会有95%的概率血本无归。
那怎么办呢?
把个体的不确定性,变成群体的确定性。
这就是“大数定律”。
你抛一枚均匀的硬币,落地后正面向上,或者反面向上的概率,都是50%。
那么你抛两次硬币,就一定会出现一次正面向上,一次反面向上吗?
不一定。
但是如果你抛1000次呢?
结果几乎就是一定的了。
正面向上和反面向上的次数,都接近于500次。
只要你重复实验的次数足够多,最终的结果就会比较稳定,趋近于期望值。
风险投资,也是这个道理。
假如一个人创业,成功的概率是5%。我投资他一个人,有95%的概率血本无归。
那如果我投资20个这样的人呢?
20个人中,只要有1个人创业成功了,我就能赚到超过20倍的钱,对我来说就是划算的。
那么,20个人中,至少有1个人成功的概率是多少?
是64.2%。(1-0.95^20=64.2%)
投资1个人,我投资成功的概率是5%。
而投资20个人,我投资成功的概率是64.2%。
我投资成功的概率就大大增加了。
这就是风险投资的逻辑。
在真实的商业世界中,每个创业者的个人水平不同、选择的赛道不同、商业的逻辑也不同。
他们的成功概率都是不同的。有的人成功概率是1%,有的人是5%,而有的人是8%。
但总体来说,创业是九十九死一生的游戏。5%的成功概率,已经算是高的了。
投资人所做的事情,就是靠自己的经验和眼光,筛选出那些成功概率更高、回报倍数更高的人。
然后,一次去投很多很多人,分散风险。
这样他们大概率就能投资成功,获得巨大的回报。
这就是把个体的不确定性,变为群体的确定性。
风险投资,就是这样系统地靠大数定律赚钱的。
7
如果,在学生时代,你对数学老师说:
老师,我觉得数学一点用都没有。我不明白,学数学,到底是为了什么?
我相信,大部分的数学老师,可能都会给出一个同样的回答:
学数学,是为了锻炼你的数学思维。
什么是数学思维?
比如说,我们前面说到的公理体系,就是一种几何思维。你会明白,一家企业的“大厦”,是怎样一步一步搭建出来的。
再比如说,我们前面说到的概率体系,就是一种概率思维。你会明白,正确的事,是值得重复去做的。
还有吗?
好吧。这个问题太深奥了,我实在是没有办法穷举。
再举三个例子吧。微积分、代数、博弈论。
别怕,我们一个一个来说。
很多人一听说微积分,想到那些复杂的微分方程、积分方程,就头疼。
我们今天不聊方程,只聊微积分的思维方式。
微积分的思维方式其实特别简单,也正是因为简单到了极致,所以非常漂亮。
微积分是牛顿发明的。所以,他为什么要发明微积分呢?
你可能会说,是为了在考试中虐待我们。
不是的。
其实在牛顿以前,人们对速度这些变量的了解,仅限于平均值的层面。
比如说,我知道一段距离的长短,和走完这段距离的时间,就可以算出一个平均速度。
但是,每个瞬间的速度,我是不了解的。
于是,牛顿就发明了微分,用无穷小这种概念来帮助我们把握瞬间的规律。
而积分跟微分正好相反,它反映的是瞬间变量的积累效应。
说了半天,到底什么是微积分?
我举个简单的例子。
一个物体静止不动,你推它一把,会瞬间产生一个加速度。
但有了加速度,并不会瞬间产生速度。
加速度累积一段时间,才会有速度。
而有了速度,并不会瞬间产生位移。
速度累积一段时间,才会有位移。
宏观上,我们看到的是位移。但是从最微观的角度来看,其实是从加速度开始的。
加速度累积,变成速度。速度累积,变成位移。
这,就是积分。
反过来说,物体之所以会有位移,是因为速度在一段时间的累积。
而物体之所以会有速度,是因为加速度在一段时间的累积。
位移(相对于时间)的一阶导数,是速度。
而速度(相对于时间)的一阶导数,是加速度。
宏观上,我们看到的是位移,但是从微观上来看,其实是每一个瞬间速度的累积。
而位移的导数,就是从宏观回到微观,去观察它“瞬间”的速度。
这,就是微分。
我的头…
所以,微积分跟我有什么关系?
理解了微积分,你看问题的眼光,就会从静态变为动态。
什么意思?
人类,就是微积分的例子。
你今天晚上努力学习了,但是一晚上的努力,并不会直接变成你的能力。
你的努力,得累积一段时间,才会变成你的能力。而你有了能力,也不会马上就出成绩。
你的能力,得累积一段时间,才会变成你的成绩。而你有了一次成绩,还是不会马上就得到领导的赏识。
你的成绩,得累积一段时间,才会得到领导赏识。
从努力,到能力,到成绩,到赏识,它是有一个过程的,有一个积分的效应。
日积月累,水滴石穿,不是尽人皆知的故事吗?
不是的。你会发现,有很多人其实并不相信这个过程。
“我今天这么努力地工作了,一分钟都没摸鱼,领导为什么还不赏识我?”
“我已经推过这个飞轮了,为什么它还没有转起来?”
他忘记了。忘记了过程的力量。
反过来说,有些人可能一直以来工作都做得特别好。但是从某个时候开始,因为一些原因,慢慢开始懈怠了。
他的努力程度下降了。但这个时候,他的能力并不会马上跟着下降。可能过了三四个月,才会慢慢显示出来。
他会发现,做事情开始变得不能从心所欲了。然后又过了三四个月,他做出来的东西,领导开始越来越看不上了。
他可能会觉得,这有什么大不了的,我不过就是这一件事没做好呗。
但他忘记了。忘记了这仍然是一个“过程”。
早在七八个月前他不努力的时候,一切都埋下了种子。
努力的时候,都希望瞬间被认可。
出事的时候,却不去想几个月之前就开始忽视的蚁穴。
8
聊完微积分,我们再来聊聊代数。
一开始,我们学的是自然数,包括0和正整数。0,1,2,3,4,5…
然后是整数,包括了自然数和负整数。…-3,-2,-1,0,1,2,3…
然后是有理数,包括了整数和分数。
在学习分数之前,数字在我们的认知中,是离散的,是数轴上一个又一个的点。
而有了分数,数字就开始变得连续了。
有理数之后,我们又学了无理数。无理数,就是无限不循环小数,比如π。
任何一个有理数,都可以由两个数相除而得来。但是无理数是无限不循环的小数,你找不到任何规律。
你会相信,世界不只是对和错、大和小。点和点之间,还有一个充满灰度的空间。
你会相信,在这个世界上,有些事情就是复杂到没有规律的。
π就是π,根号就是根号,它就是很复杂,复杂到没有任何一个简单粗暴的方式能来定义它。
你要承认它的客观存在,承认这个世界的复杂性。
你看,我们就是在各种数里,一步一步地理解了这个复杂的世界。
再复杂一点。数这个东西,除了大小,其实还有一个非常重要的属性:方向。
在数学上,我们把有方向的数字叫做向量。
数字,还非得加个方向,有意义吗?
我举个例子。
假如,你今天拖着一个箱子往东走。你力气很大,有3000N。
这时,有人非要跟你对着干。他把箱子往西拖,但力气没你大,只有2000N。
结果呢?
这个箱子还是会跟着你往东走,只不过只剩下1000N的力,它的速度会慢下来。
可如果拖着的不是箱子,而是人呢?
两位得力战将,向着完全相反的方向发力。与其互相牵制,那可能还不如完全交给其中一个人来做。
这挺容易理解。但还有一种情况。
做同一件事情,有的人想往东走,有的人想往西走,有的人想往北走,你呢?
你并不知道哪个方向是正确的。
那怎么办?
你就让他们都去干这件事吧。
虽然大家的方向不同,会互相牵制,力的大小会有损耗。
但是最终事情的走向,会是那个相对正确的方向。
9
最后,我们来说说博弈论。
什么是博弈论?
我们每天都要做很多很多大大小小的决策。
比如说,我午饭是吃饭、吃面、还是吃饺子?
这就是一个决策。
这个决策只跟我自己有关,并不会涉及到别人。
但总有一些决策,是需要涉及到别人的。
涉及到别人的决策逻辑,我们把它叫做博弈论。
比如说,围棋。
每走一步棋,我的所得就是你的所失,我的所失就是你的所得。
这是博弈论中典型的零和博弈。
在零和博弈中,你要一直明白,你要的是全局的最优解,而不是局部的最优解。
什么意思?
下围棋的时候,不是在每一步上,你都要吃掉对方最多的子。
你要让终局所得最多,就要步步为营,讲究策略。
有时候让子是为了以退为进。始终记得,你是为了全局最优,而不是局部最优。
这就是所谓的,善弈者,通盘无妙手。
创业如是,商业如是,人生亦如是。
不要总想着每一件事情都必须一帆风顺,如果你想得到最好的结果,可能在一些关键步数上就要做些妥协。
除了零和博弈,还有一种博弈,叫做非零和博弈。
非零和博弈讲究共赢。
共赢的前提,是建立信任。但建立信任,其实特别不容易。
为什么?因为考验人性。
假如,市场上现在需要100万台冰箱。
一个厂家发现了这个需求,决定马上生产100万台。
另一个厂家发现了这个需求,也决定马上生产100万台。
第三个厂家也是一样。
……
结果,每一个厂家都生产了100万台,供大于求,大部分厂家都会遭受很大的损失。
如果这个时候,大家能够建立起信任,说好10个厂家,每个人都只生产10万台,这样正好能够满足需求,每个厂家都能够赚到钱,大家就能达成共赢。
你看,大团圆结局。
可是,你很清楚,总会有人打破约定的。凭什么要求我只生产10万台?我偏不。
只要有一个厂家没有遵守约定,别人都生产10万台,但是他生产30万台,这个时候,就多出来了20万台,大家就会因此遭受损失。
建立这种信任,特别不容易,但是这件事情在商业世界里非常重要。
那怎么才能建立信任呢?
我斗胆提两个建议。
第一个建议是,你要找到那些能够建立信任的伙伴。
有些人,是永远都无法和他达成共赢的,这样的人你就要远离。
第二个建议是,你要主动释放信任。
你要先让别人知道你是值得信任的人,这样想要与你达成共赢的人,才会来找到你。
最后的话
数学的星空,太浩瀚了。
28年前,1994年那个炎热的夏天,是属于我的高考季。
在拿到622分的成绩单之后,我和千千万万个少年一同面对着一件人生大事。
填志愿。选学校。选专业。
南京大学,是我梦寐以求的高校。国际金融,是那一年的大热专业。
可我身边那些超级学霸们都选择了计算机。我也执拗地认为,计算机才是未来的趋势。
于是,我也满怀着对未来的憧憬,填下了“南京大学,计算机专业”。
是的。数学,不是我的第一志愿。
然后…分没够上。
可无比幸运的是,那一年,南京大学的投档线,是618分。
将将比我的成绩低了4分。
简单来说就是…我被调剂了。
就这样,我混进了南京大学,鬼使神差地成为了一个数学系的学生。(当然,我还是很喜欢数学的,小的时候还拿过全国数学竞赛的一等奖。)
如果当年,我顺利地被南京大学计算机系录取了,我的人生会变成什么样呢?
我不知道。
我能知道的是,我是数学的受益者。
它是我的热爱,是我的工作,是我的思维,是我的底层逻辑。
所以,谢谢。
真的真的,谢谢你们,我的每一任数学老师。
谢谢你们。