一个数学家要想在普通人面前显摆自己的聪明才智,最有效的办法就是出一道关于无穷的数学题。比如,数学家问你:“1/2+1/4+1/8+1/16+……+1/(2的n次方,n=无穷大)=?”你想了想,回答说,等于1。“那么,你能证明吗?”数学家挑战性地问。你回答不出来。数学家得意地拿出一张早已画好的草图给你看:
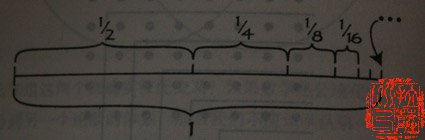
“很明显,n越大,线段的总长度加起来就越接近1。当n等于无穷大的时候,线段长度就等于1了。”数学家说:“古代人就是用这个办法算π值的。比如,古罗马时代留下了一枚戒指,上面的图案是这样的。”
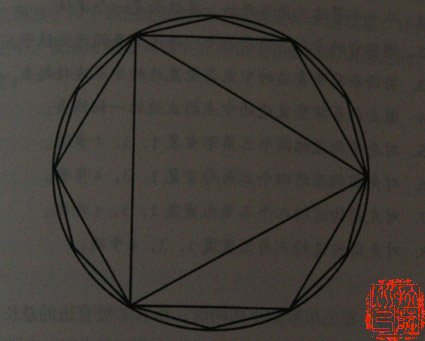
“这幅图的意思是说,一个圆可以被分成正n边型,n越大,n边型的周长就越接近圆周长。n边型是可以用几何方法算出来的,只要n足够大,得出的π值就越接近真正的π值,对吧?”
你点头称是,以为自己终于理解了无穷大的妙处。然后,数学家拿出了杀手锏。“再请看下面这张图。”
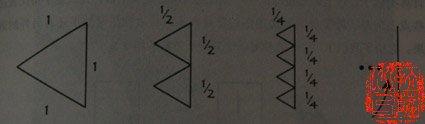
“最左边的图是等边三角形,边长假定为1。下一张图右边的线段长度仍然是1,左边被分成两个相等的等边三角形,边长是1/2。4条边总长度加起来是2。图3更近一步,把等边三角形分成4份,右边仍然是1,左边的锯齿总长度则还是2。依此类推下去,当把三角形分成无穷多份的时候,右边仍然是1,左边按理说应该还是2。但是,此时左边变成了几乎看不出来的细小的锯齿,总长度看起来变成了1。于是,这张图证明:1=2。”
这回轮到你傻眼了。1肯定不等于2,这是你从生下来就知道的常识。但是……你想不明白问题到底出在哪里。
上面这个故事选自一本通俗数学书,名叫《雨林中的欧几里德》。作者约瑟夫·马祖尔告诉读者,一般人的大脑中天生就存有数学的基本概念,比如1+1=2,两点之间只能画一条直线……诸如此类,我们可以称之为数学直觉。整座经典数学的大厦,都是基于少数几个数学直觉,我们称之为公理。这些公理之所以不需要证明,是因为人类从日常生活中早已千百次体会到了它们的准确性,因此在进化的过程中被固定在了大脑中。
但是,当数学介入无穷大的范畴时,人类的直觉就不管用了。这时就必须抛开直觉,换用另一套思维方式。比如上述1=2的问题,就是通过微积分来解决的。普通人不能仅凭直觉理解微积分,必须变换思路才行。
类似的思想,可以引申到日常生活的很多方面。比如,《科学美国人》杂志的专栏作家michael shermer 最近写了一篇文章,试图解释人类为什么经常容易犯统计错误。比如,你昨晚梦到某人,结果今天他就出了车祸,于是你觉得自己有了特异功能。其实呢,人类平均每晚要做5个梦,假定我们只能记住其中的十分之一,全中国加起来每天也会有6.5亿个梦被记住。假定其中有十分之一是关于某位朋友的,那么全中国每天被记住的关于朋友的梦就有6500万个!这样一算,你还会觉得发生在自己身上的这次异灵事件很少见吗?
但是,大部分人不会这么算,他们会牢记那一次“异灵事件”,继而相信特异功能,或者别的什么神秘的理论。这是为什么呢?著名的科普作家理查德·道金斯提出一个说法,他认为人类生活的世界是一个“中间世界”,原子核内发生的事情对我们没有关系,我们不需要理解它们。同样,宇宙间发生的事情也是如此。换句话说,人类的直觉不能理解在超大或者超小尺度上发生的事情。要想理解它们,必须抛弃自己的直觉。
随着科技的进步,人口的数量越来越大,活动的范围越来越广,人类已经不得不面对一些超级事件了。举个简单的例子:人类从来没有进化出倒时差的功能,因为人类从来就不需要。但是飞机的出现使得人类必须学会倒时差,所以倒起时差来是那么地痛苦……
上面这个例子属于生理范畴,比较不容易冒犯读者。其实在思维领域,这样的例子比比皆是,大家好好想想吧。
随便说一句,音乐也是一个很好的例子。有人说音乐是人类的普世价值,打死我也不信。就拿大家都说好的古典音乐来说,你去给一个从来没听过古典音乐的非洲人放莫扎特,他要是喜欢才奇怪呢。
如果你还不相信,那么请听下面这段钢琴曲:
这是美国著名的爵士钢琴演奏家thelonious monk演奏的《’round midnight》,1957年的录音。monk的音乐一直被形容为“有棱角的、出乎意料的、有智慧的”,因为他的音乐感觉和那个时候的大多数听惯了古典音乐的人很不一样,或者说是“违反音乐直觉的”。就拿这首曲子来说,它原来是一首人人都会哼唱的通俗小调,但monk在演奏的时候完全不按牌理出牌,你永远不会猜到他下一个音要弹什么。古典音乐里如果出现这样的音,会被认为是丑恶的。但是,当一部分听众习惯了爵士乐后,反而会特别喜欢这种出乎意料的声音。monk现在被认为是bebop爵士乐的奠基人之一,这可真不是我瞎吹的。







